문제
자연수 N과 정수 K가 주어졌을 때 이항 계수 (NK)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 4,000,000, 0 ≤ K ≤ N)
출력
(NK)를 1,000,000,007로 나눈 나머지를 출력한다.
예제 입력 1 복사
5 2
예제 출력 1 복사
10
*문제 해석
이항계수 문제다. nCk를 1,000,000,007로 나눈 나머지를 출력하면 된다.
nCk = n! / (n-k)! k!
이를 재귀 팩토리얼을 통해 풀려고 하면 스택오버플로우로 인해 계산하지 못하게 된다. 시간복잡도가 O(n^2)인데 n의 범위가 범위가 4백만이라 상당 크다. 시간초과가 걸린다.
그래서 방법을 찾던중 '페르마의 소정리' 라는 것을 알게 되었다.
<페르마의 소정리>

첫째줄 3번째 조건은 a가 소수p의 약수가 아니란 뜻이다.
3번째 줄을 이용한다면 다음과 같은 수식을 얻을 수 있다.
( a^(p-2) = 1/a * (mod p) (a != 0) )
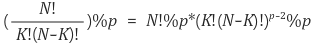
이는 나머지 연산의 분배법칙에 의해서 구해진 것이다.
(A + B) % p = ((A % p) + (B % p)) % p
(A x B) % p = ((A % p) x (B % p)) % p
(A - B) % p = ((A % p) - (B % p) + p) % p
그러면 코딩은 팩토리얼과 거듭제곱을 함수로 구현하고, 그것을 페르마의 소정리 형태로 호출하면 될 것이다.
*나의 코드
import sys
input = sys.stdin.readline
N,K = map(int, input().split())
p = 1_000_000_007
# 팩토리얼(나머지 적용)
def factorial(t):
n = 1
for i in range(2, t+1):
n = (n * i) % p
return n
# 거듭제곱(나머지 적용)
def square(n, k):
if k == 0:
return 1
elif k == 1:
return n
tmp = square(n, k//2)
if k % 2:
return tmp * tmp * n % p
else:
return tmp * tmp % p
top = factorial(N)
bottom = factorial(N-K) * factorial(K) %p
#페르마의 소정리 적용
print(top * square(bottom,p-2) %p)
*중요한 점
이 문제의 핵심은 '페르마의 소정리'다. 확실히 기억해두도록 하
페르마의 소정리를 활용해 분수형태를 곱셈으로 한 뒤 모듈로 연산의 곱에 대한 분배법칙을 활용하는 것이 중요하다.
'코딩테스트 > 백준' 카테고리의 다른 글
| 21. 백준 2470 (골드5) : 두 용액 _ python풀이 / 정렬 (0) | 2024.09.08 |
|---|---|
| 20. 백준 1904 (실버3) : 01타일 _ python풀이 / DP (0) | 2024.09.03 |
| 18. 백준 5639 (골드4) : 이진검색트리 _ python풀이 / 이진트리 (0) | 2024.09.01 |
| 17. 백준 10158 (실버3) : 개미 _ python풀이 / 애드 혹 (0) | 2024.08.31 |
| 16. 백준 9663 (골드4) : N-Queen _ python풀이 / 브루트포스 (0) | 2024.08.30 |

